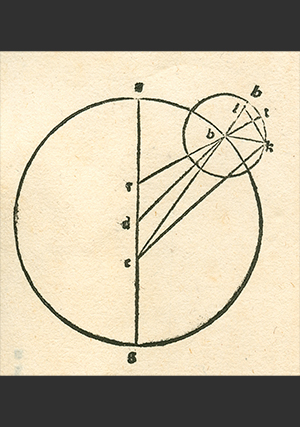
Ptolemy’s Planetary Model

- Ptolemy, Almagest XI.9: equant diagram.
- Par. gr. 2389 (IX cent.), f. 306v; Paris, Bibliothèque nationale de France (BNF).

- Gerard of Cremona, translation of Ptolemy’s Almagest.
- Ptolemy, Almagest XI.9: equant diagram.
- Almagestum Cl.Ptolemei Preludiensis Alexandrini Astronomorum Principis. Opus Ingens ac Nobile Omnes Celorum Motus Continens (Tr: Gerardus Cremonensis).
- Venice: Peter Liechtenstein, 1515; fol. 127r.
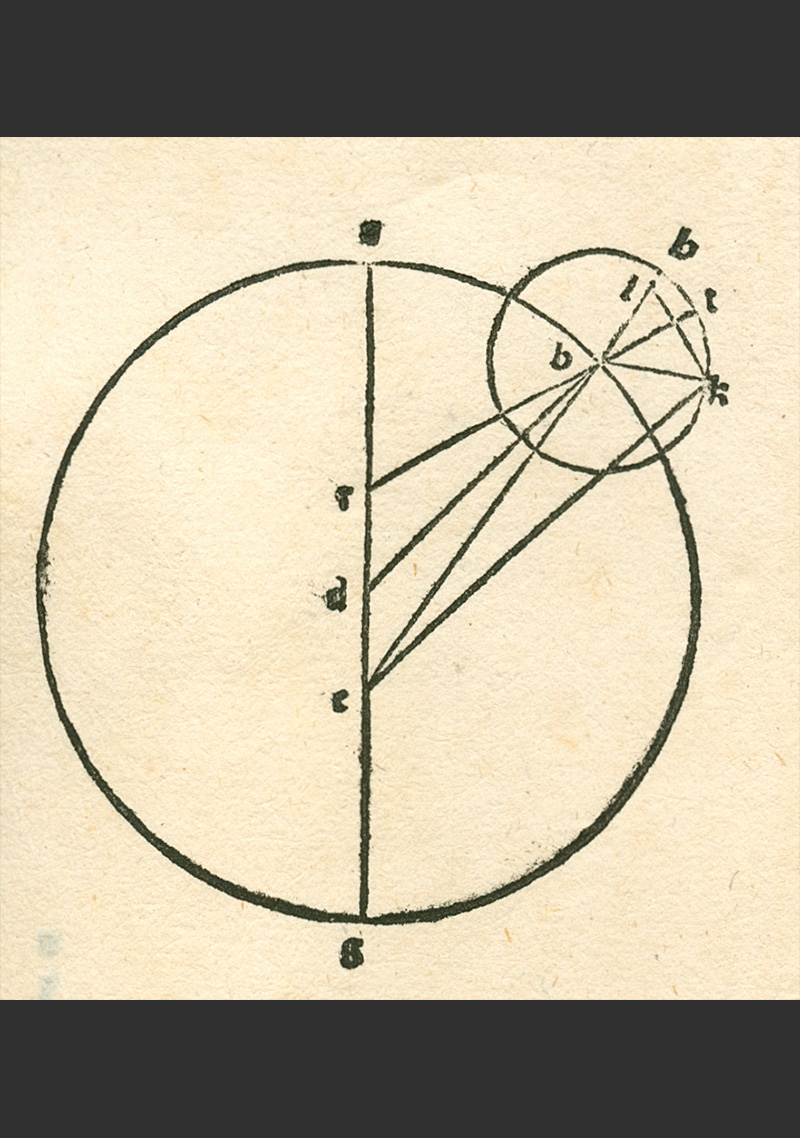
- Gerard of Cremona, translation of Ptolemy’s Almagest.
- Ptolemy, Almagest XI.9: equant diagram (detail).
- Almagestum Cl.Ptolemei Preludiensis Alexandrini Astronomorum Principis. Opus Ingens ac Nobile Omnes Celorum Motus Continens (Tr: Gerardus Cremonensis).
- Venice: Peter Liechtenstein, 1515; fol. 127r.
This diagram from chapter 9 of book XI of Ptolemy’s Almagest depicts his equant model for an outer planet. Two versions of the diagram are shown here, one from one of the most important Greek manuscripts of Ptolemy (see the first image) and the other from the Latin translation by Gerard of Cremona (see the second image).
A major goal of ancient Greek astronomy was to find geometrical models which could account for the irregular motion of the planets. There are two principal irregularities (or anomalies) which needed to be explained. The most obvious is that for a period of time the planet changes the direction of its motion and moves backwards (‘retrograde’) through the fixed stars. Less immediately obvious, but still easily observable, is the fact that the speed of a planet’s motion changes. Both irregularities are at odds with the idea that a planet moves with constant speed along a circular orbit centered on the Earth.
The solution proposed by Greek astronomers to the problem of accounting for these irregularities in the motion of the planets was to consider the combined effect of motion around more than one circle. The simplest form of such motion is called the epicycle-deferent model. In this model, the planet moves around a small circle called the epicycle whose center is itself moving in the opposite direction around a larger deferent circle. With appropriate choices of the relative sizes of the two circles and the speeds of rotation on the two circles, such a model can produce changing speeds and retrograde motion. However, the resulting motion is still too regular. In particular, the duration of retrograde motion and the length of the retrograde arc is constant in a simple epicycle-deferent model. Observation, however, shows that the retrograde arc changes depending upon which part of the zodiac the planet is located in at that time.
Ptolemy proposed an ingenious two-part solution to this problem. First, he moved the Earth away from the center of the deferent circle. As a result, because the distance of the center of the epicycle from the Earth changes as the epicycle moves around the deferent, the retrograde arcs will appear to be longer and shorter as viewed from the Earth. But this correction to the model was not sufficient — the model produced better agreement with the observed motion of a planet, but there were still significant discrepancies. Ptolemy therefore added an additional factor into his model. He introduced a geometrical point diametrically opposite to the Earth from the center of the deferent circle about which the epicycle appeared to move with constant speed. The epicycle therefore no longer moved with constant speed around the center of the deferent, but instead speeded up and slowed down as it moved around the deferent. Viewed from the Earth, this effect was even greater. In modern terms, the effect of the equant is to approximate constant motion around an ellipse rather than around a circle.
Ptolemy’s equant model replicates the motion of a planet remarkably accurately. Using observations to determine the parameters of the model (the relative sizes of the deferent and epicycle, the speeds around the two circles, and the distance of the Earth and the equant point from the center of the circle), he was able to produce tables for calculating planetary positions that were much better than those previously known. But his model was not without its critics. By introducing the equant point, Ptolemy broke the golden rule of Greek geometrical astronomy, namely that motions should be accounted for by uniform (i.e., constant speed) circular motion. Ptolemy must have known this but stayed silent on the point. But later astronomers, especially in the Islamic world but also European astronomers such as Copernicus, strongly objected to this aspect of Ptolemy’s model. These astronomers came up with ingenious, but often complicated, models using combinations of only circular motions to reproduce the effect of Ptolemy’s equant point.
Not all later astronomers fully understood Ptolemy’s model. The diagram in the Latin translation (see detail) accurately reflects Ptolemy’s model: the center of the epicycle (labelled b) moves around the deferent circle with center d. The Earth is located away from the center of the deferent at c and the equant point is placed directly opposite at r. However, in the Greek manuscript, the Earth (Ε) is wrongly placed at the center of the deferent circle, the actual center of the deferent (Δ) is located off-center rather than at the center; the equant point (Ζ) is correctly placed opposite the Earth on a line passing through the center of the deferent circle.
Select Bibliography
- Neugebauer, Otto. 1975. A History of Ancient Mathematical Astronomy. Studies in the History of Mathematics and Physical Sciences. 1. New York: Springer-Verlag: pp. 170–183.
- Pedersen, Olaf, and Alexander Jones. 2011. A Survey of the Almagest. Revised edition. New York: Springer: 261–294.
- Toomer, Gerald J. 1984. Ptolemy’s Almagest. New York: Springer-Verlag.